QPHIL: Quantizing Planner for Hierarchical Implicit Q-Learning

Alexi Canesse*,†,1, Mathieu Petitbois*,2, Ludovic Denoyer3, Sylvain Lamprier4, Rémy Portelas2
1Ecole Normale Supérieure de Lyon, 2Ubisoft La Forge 3H Company 4University of Angers
*Equal contribution, †Work done during an intership at Ubisoft La Forge
Paper Code Datasets & Models

Abstract

Offline Reinforcement Learning (RL) has emerged as a powerful alternative to im itation learning for behavior modeling in various domains, particularly in complex long range navigation tasks. An existing challenge with Offline RL is the signal- to-noise ratio, i.e. how to mitigate incorrect policy updates due to errors in value estimates. Towards this, multiple works have demonstrated the advantage of hier archical offline RL methods, which decouples high-level path planning from low- level path following. In this work, we present a novel hierarchical transformer- based approach leveraging a learned quantizer of the state space to tackle long horizon navigation tasks. This quantization enables the training of a simpler zone-conditioned low-level policy and simplifies planning, which is reduced to discrete autoregressive prediction. Among other benefits, zone-level reasoning in planning enables explicit trajectory stitching rather than implicit stitching based on noisy value function estimates. By combining this transformer-based planner with recent advancements in offline RL, our proposed approach achieves state-of- the-art results in complex long-distance navigation environments.

1. Scaling Offline GCRL to Long‑Range

Challenge: Learn a policy $\pi(a\mid s,g)$ from imperfect demonstrations $\mathcal{D}=\{\tau\}$ that reaches goal $g$ from state $s$ offline.

Limits: Value‑based RL suffers from noisy estimates, especially for long horizons.

Question: How can we reduce value‑function noise while keeping strong path‑following performance?

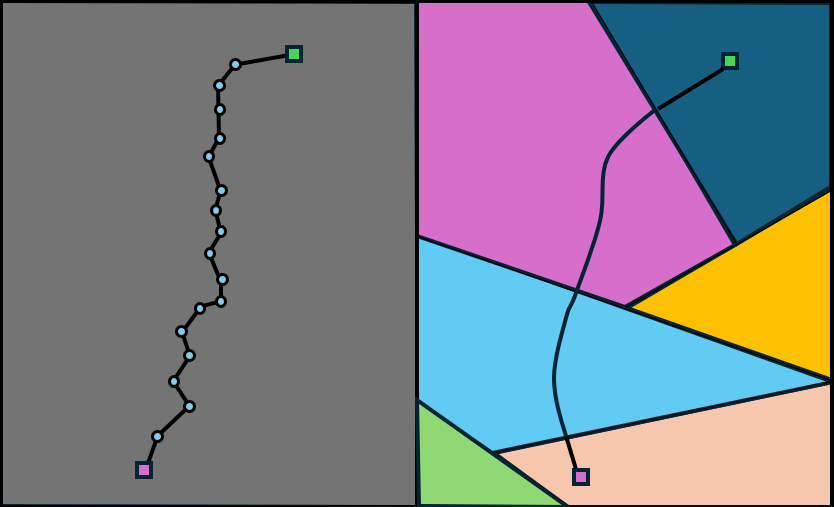
intro1
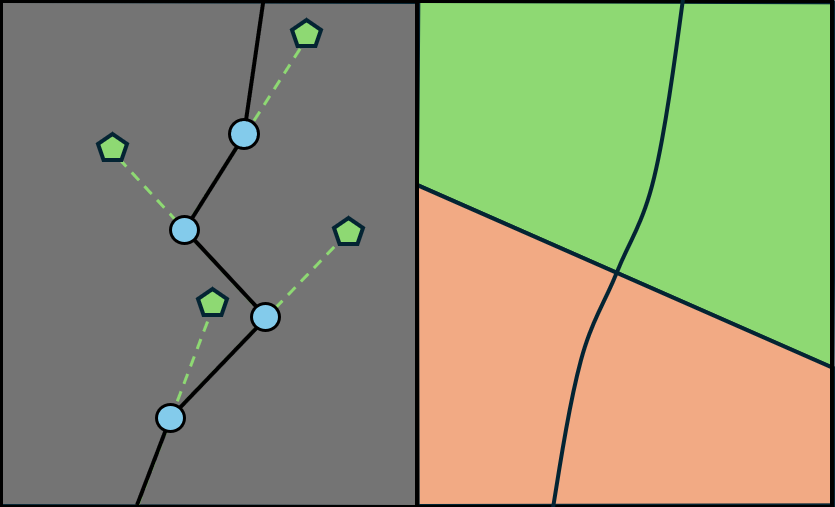
intro2
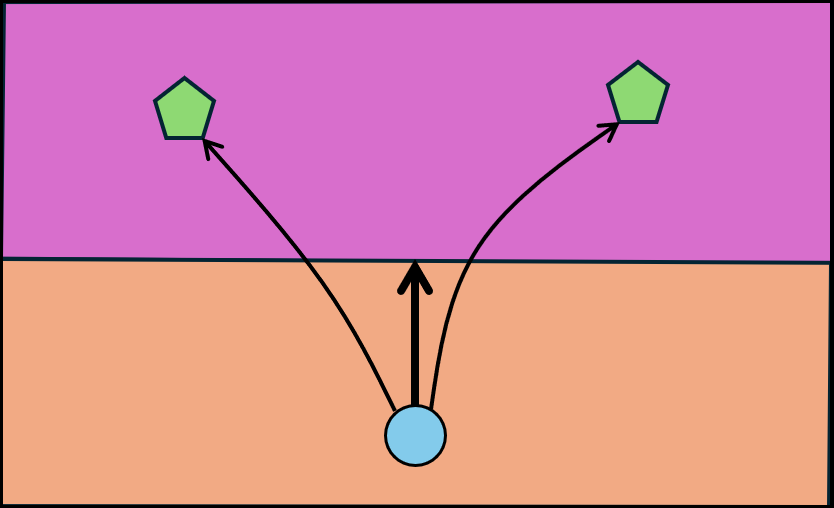
intro3

QPHIL learns discrete landmarks and leverages them to:

  • • Simplify sub‑goal planning with discrete tokens.
  • • Avoid noisy high‑frequency sub‑goal updates.
  • • Relax conditioning from sub‑goals to landmarks.

2. QPHIL: Architecture & Inference

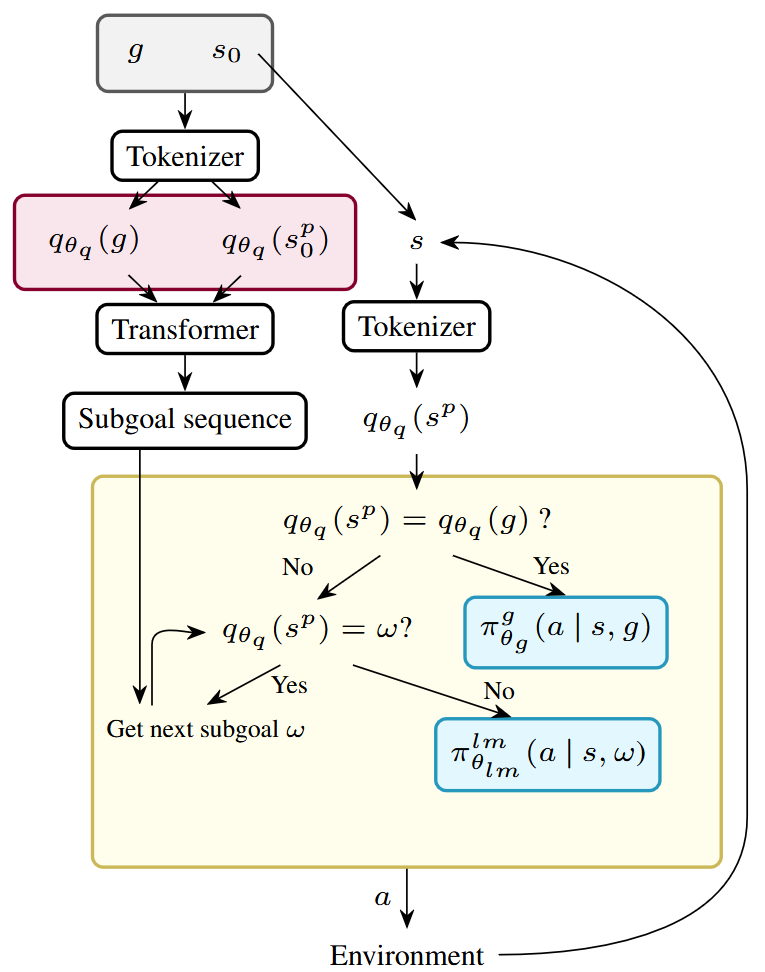
open loop

Open‑loop inference pipeline

QPHIL operates through four components:

Quantizer: $q_{\theta_q}$ discretises states & goals.
Planner: $\pi^{p}_{\theta_p}$ predicts landmark plans.
Landmark policy: $\pi^{lm}_{\theta_{lm}}$ executes plans.
Goal policy: $\pi^{g}_{\theta_{g}}$ finalises within last landmark.

3. QPHIL: Training & Losses

QPHIL components are trained sequentially:

Quantizer $q_{\theta_q}: \mathcal{S}^p \to \Omega$ with encoder $f^e_{\theta_e}$ and codebook $z$, learned by minimizing $\mathcal{L}_{\text{quantizer}}$, combination of Contrastive loss $\mathcal{L}_{\text{contrastive}}$ and VQ‑VAE loss $\mathcal{L}_{\text{VQ‑VAE}}$.

Planner $\pi^{p}_{\theta_p}: \Omega_H \times \Omega \to \Omega_P$, learned by minimizing the log‑likelihood loss $\mathcal{L}_{\text{planner}}$ over compact landmark sequences.

Landmark policy $\pi^{\text{lm}}_{\theta_{lm}}$ and Goal policy $\pi^{g}_{\theta_{g}}$ are learned with Implicit Q‑Learning (IQL).

4. Environments & Datasets

Environments: AntMaze (Medium, Large, Ultra, Extreme)

Ant robot
Maze maps
Quantization

Datasets: trajectories $\mathcal{D}$ of two types:

  • Diverse: random start / goal positions.
  • Play: curated start / goal positions.

5. Key Results

QPHIL on AntMaze: scales with navigation range, matching SOTA on small mazes and greatly surpassing prior work on harder ones.

EnvironmentGCBCGCIQLGCIVLHGCBC
w/o repr		HGCBC
w/ repr		HIQL
w/o repr		HIQL
w/ repr		QPHIL
medium‑diverse65±1180±882±846±1113±992±492±492±4
medium‑play 60±1180±984±948±910±890±592±491±2
large‑diverse 10±521±1059±1378±718±888±485±882±6
large‑play 9±525±1250±979±714±1387±784±780±3
ultra‑diverse 16±920±86±571±1232±2471±771±1262±7
ultra‑play 15±1020±1010±664±1213±1563±2074±2362±4
extreme‑diverse9±612±75±106±140±414±1720±2040±13
extreme‑play 8±716±70±011±104±812±1628±2750±7

6. Ablations

  • Contrastive loss is crucial for good quantization and performance.
  • VQ‑VAE reconstruction loss eases hyper‑parameter tuning.
  • Success rate plateaus beyond a reasonable codebook size.
  • Out‑of‑distribution positions share landmarks with neighbours.
  • Under diverse initial states/goals, QPHIL still performs.

7. Conclusion

QPHIL leverages learned landmark representations to achieve state‑of‑the‑art long‑range planning on offline GCRL navigation benchmarks.

Limits: Currently focused on navigation; may not transfer to more intricate planning domains.

Future work: Scale landmark dimension, tackle higher‑dimensional problems, and exploit QPHIL’s interpretability.