Offline Learning of Controllable Diverse Behaviors

Abstract

Imitation Learning (IL) techniques aim to replicate human behaviors in specific tasks. While IL has gained prominence due to its effectiveness and efficiency, traditional methods often focus on datasets collected from experts to produce a single efficient policy. Recently, extensions have been proposed to handle datasets of diverse behaviors by mainly focusing on learning transition-level diverse poli- cies or on performing entropy maximization at the trajectory level. While these methods may lead to diverse behaviors, they may not be sufficient to reproduce the actual diversity of demonstrations or to allow controlled trajectory generation. To overcome these drawbacks, we propose a different method based on two key features: a) Temporal Consistency that ensures consistent behaviors across entire episodes and not just at the transition level as well as b) Controllability obtained by constructing a latent space of behaviors that allows users to selectively activate specific behaviors based on their requirements. We compare our approach to state-of-the-art methods over a diverse set of tasks and environments.

1. Diverse Behavior Learning

Challenge: Generating the same trajectory distribution $p_{\mathcal{M},\mu}(\tau)$ as in a dataset $\mathcal{D}_e$ generated by the experts $\Pi_e = \{\pi_e^{(1)}, \pi_e^{(2)}, \ldots, \pi_e^{(k)}\}$ with $1\le k \le |\mathcal{D}_e|$ in a fully offline manner.

Limits: Traditional imitation learning such as Behavior Cloning (BC) fails when $k>1$ because it captures only transition‑level diversity.

Question: How to learn from $\mathcal{D}_e$ a policy $\pi$ capable of:

• Diversity: Reconstructing the trajectory distribution?
• Controllability: Being prompted to generate specific behaviors?
• Robustness: Displaying robustness to compounding errors and environment stochasticity?

2. ZBC: Stylized BC

ZBC addresses Diversity & Controllability by minimising

$$ \mathcal{L}_{ZBC}(\theta) = -\mathbb{E}_{\textcolor{blue}{\tau_i}\sim \mathcal{D}}\Bigl[\,\mathbb{E}_{(\textcolor{blue}{s_t^i},\textcolor{blue}{a_t^i})\sim \textcolor{blue}{\tau_i}}\bigl[\log\pi_{\theta}(\textcolor{blue}{a_t^i}\mid \textcolor{blue}{s_t^i},\textcolor{blue}{z_i})\bigr]\Bigr]. $$

and reconstructing

$$ p_{\mathcal{M},\pi_{\theta}}^{ZBC}(\tau)=\frac{1}{|\mathcal{D}_e|}\sum_{\textcolor{blue}{i}=0}^{|\mathcal{D}_e|-1}p_{\mathcal{M},\pi_{\theta}(\cdot\mid\cdot,\textcolor{blue}{z_i})}(\tau). $$

Yet compounding errors and environment stochasticity can create OOD $(s,z)$ pairs, and ZBC tends to over‑fit.

3. WZBC: Weighted Stylized BC

WZBC achieves Diversity, Controllability and Robustness with

$$ \mathcal{L}_{WZBC}(\theta) = -\mathbb{E}_{(\textcolor{blue}{\tau_i},\textcolor{red}{\tau_j})\sim \mathcal{D}}\Bigl[\,\mathbb{E}_{(\textcolor{blue}{s_t^i},\textcolor{blue}{a_t^i})\sim \textcolor{blue}{\tau_i}}\bigl[e^{-\beta\,\nu(\textcolor{blue}{\tau_i},\textcolor{red}{\tau_j})}\,\log\pi_{\theta}(\textcolor{blue}{a_t^i}\mid \textcolor{blue}{s_t^i},[\textcolor{red}{z_j}]_{i\neq j})\bigr]\Bigr]. $$

where the style–distance $\nu$ is

$$ \forall (\textcolor{blue}{\tau_i},\textcolor{red}{\tau_j})\in \mathcal{D}_e:\;\;\nu(\textcolor{blue}{\tau_i},\textcolor{red}{\tau_j}) = \frac{\left\|\operatorname{pad}(\textcolor{blue}{\tau_i^s})\!-\!\operatorname{pad}(\textcolor{red}{\tau_j^s})\right\|}{\displaystyle\max_{\textcolor{green}{\tau_k}\in \mathcal{D}_e}\left\|\operatorname{pad}(\textcolor{blue}{\tau_i^s})\!-\!\operatorname{pad}(\textcolor{green}{\tau_k^s})\right\|}. $$

4. Environments & Datasets

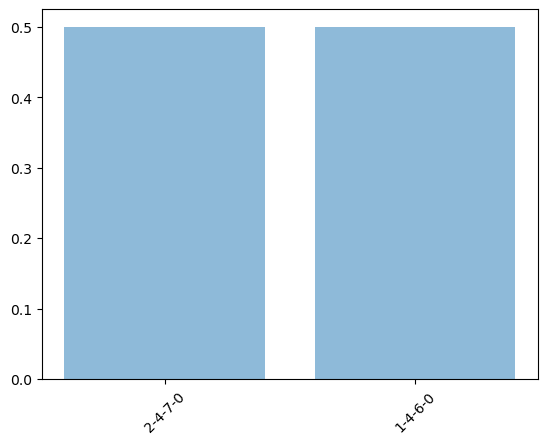
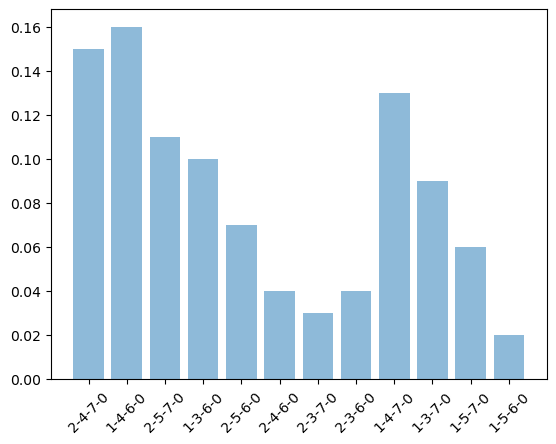
Maze2D (One‑side k=2, Only‑forward k=12)

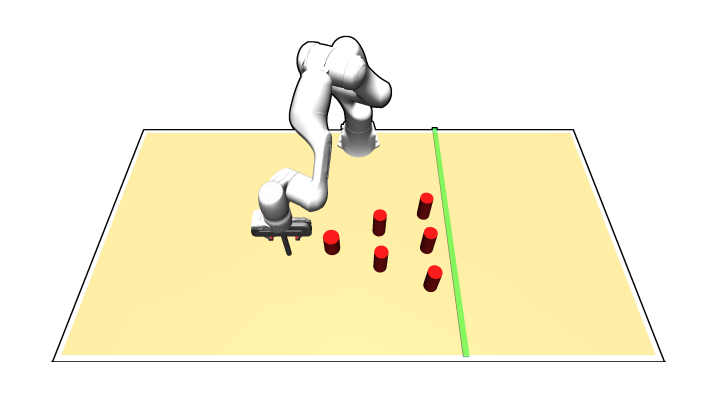
D3IL (Avoiding k=24, Aligning k=2)

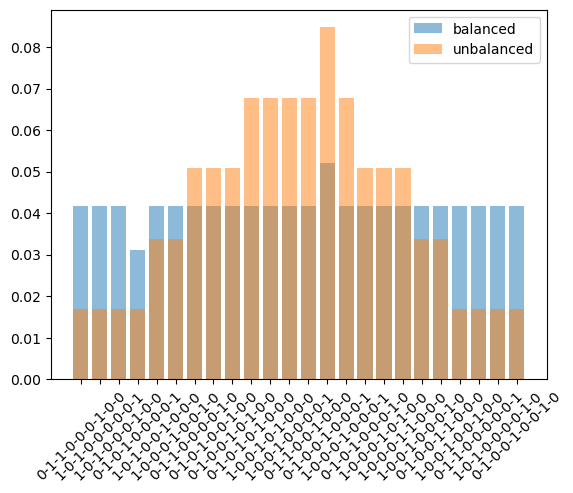
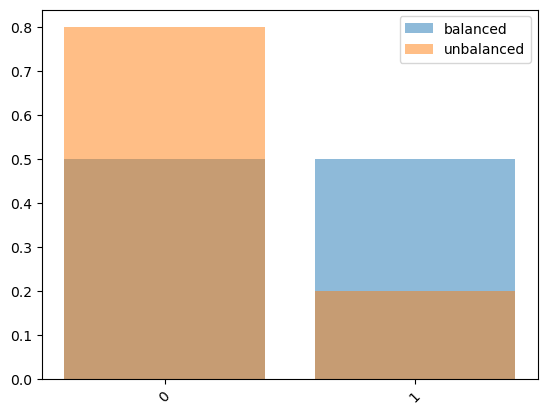
With the balanced datasets from D3IL and unbalanced datasets from their filtered versions.

5. Diversity Results

Evaluating ZBC and WZBC diversity capture. ZBC generates behaviour histograms with the lowest L₁-distance to $\mathcal{D}_e$, yet attains lower performance in more complex settings. WZBC is slightly less precise but succeeds more often.

Dataset (distance)	BC	ZBC	WZBC	BESO	DDPM‑ACT	DDPM‑GPT
medium_maze-only_forward	1.74 ± 0.054	0.256 ± 0.023	0.248 ± 0.047	0.744 ± 0.041	0.916 ± 0.252	0.604 ± 0.082
medium_maze-one_side	1.4 ± 0.49	0.044 ± 0.032	0.06 ± 0.033	0.140 ± 0.049	0.640 ± 0.390	0.100 ± 0.075
d3il_avoiding	1.917 ± 0.0	0.265 ± 0.0	0.482 ± 0.026	0.901 ± 0.091	0.781 ± 0.184	0.531 ± 0.093
d3il_unbalanced_avoiding	1.925 ± 0.062	0.102 ± 0.116	1.457 ± 0.087	1.283 ± 0.067	1.342 ± 0.134	1.26 ± 0.022
d3il_aligning	1.0 ± 0.0	0.172 ± 0.17	0.552 ± 0.224	0.472 ± 0.111	0.488 ± 0.075	0.296 ± 0.104
d3il_unbalanced_aligning	0.4 ± 0.0	0.172 ± 0.057	0.364 ± 0.037	0.256 ± 0.066	0.212 ± 0.053	0.288 ± 0.063

Dataset (success rate)	BC	ZBC	WZBC	BESO	DDPM‑ACT	DDPM‑GPT
medium_maze-only_forward	1.0 ± 0.0	1.0 ± 0.0	0.99 ± 0.0	0.998 ± 0.004	0.9 ± 0.12	1.0 ± 0.0
medium_maze-one_side	0.6 ± 0.49	1.0 ± 0.0	1.0 ± 0.0	1.0 ± 0.0	0.994 ± 0.012	1.0 ± 0.0
d3il_avoiding	1.0 ± 0.0	0.996 ± 0.005	0.954 ± 0.024	0.998 ± 0.008	0.904 ± 0.08	0.986 ± 0.006
d3il_unbalanced_avoiding	0.6 ± 0.49	0.75 ± 0.092	0.802 ± 0.113	1.0 ± 0.0	0.996 ± 0.005	0.999 ± 0.0
d3il_aligning	0.21 ± 0.395	0.52 ± 0.432	0.806 ± 0.105	0.910 ± 0.12	0.872 ± 0.047	0.852 ± 0.055
d3il_unbalanced_aligning	1.0 ± 0.0	0.328 ± 0.054	0.762 ± 0.126	0.922 ± 0.013	0.882 ± 0.038	0.844 ± 0.015

6. Controllable Generation

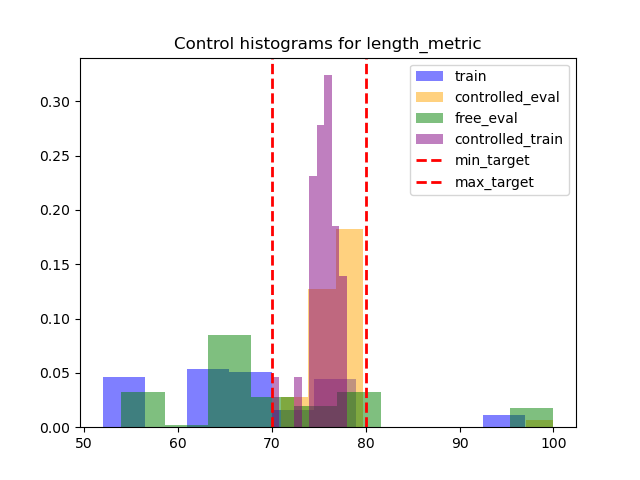
Control histograms for length_metric — Control histograms for `length_metric`

For control we :

Select trajectory styles in $\mathcal{D}_e$ that satisfy a property $\Psi(\tau)$ with $\Psi(\tau)=\bigl(\text{length}(\tau)\!\in[70,80]\bigr)$.
Generate adequate trajectories by conditioning $\pi$ on the selected styles.

7. Robustness to Stochasticity

Evaluating ZBC and WZBC under stochastic dynamics. WZBC generally surpasses ZBC in both L₁-distance and success rate as uncertainty increases.

Configuration	L1 Distance		Success Rate
Configuration	ZBC	WZBC	ZBC	WZBC
medium_maze-only-forward (determinist)	0.256 ± 0.023	0.248 ± 0.047	1.0 ± 0.0	0.99 ± 0.0
medium_maze-only-forward (pseudo-r-init)	1.152 ± 0.094	0.828 ± 0.349	0.448 ± 0.031	0.684 ± 0.152
medium_maze-only-forward (r-init)	1.556 ± 0.079	1.552 ± 0.037	0.858 ± 0.046	0.978 ± 0.019
medium_maze-only-forward (noise-transi)	0.729 ± 0.134	0.744 ± 0.029	0.632 ± 0.066	0.744 ± 0.038

8. Conclusion

ZBC learns a style‑conditioned policy enabling trajectory diversity capture and controllable generation in a fully unsupervised offline setting. WZBC bridges BC and ZBC by mixing styles to enhance robustness.

Limits: Using simple Euclidean distance is not scalable to all observation modalities; performance can degrade in highly complex environments.

Future work: Incorporating IRL techniques for richer observation spaces and leveraging RL signals to improve task performance.